A Brief Introduction to LSTM Model
Posted By :Manish Kumar |12th June 2022
What is LSTM?
LSTM (Long short-term memory) LSTM is an artificial recurrent Neural Network (RNN) capable of learning order dependence in sequence prediction problems. LSTM has feedback connections in contrast to standard feed-forward neural networks.
What is RNN?
RNN called a Recurrent Neural Network, is a class of Neural Networks. It is the first algorithm that remembers its input, due to internal memory, in other words, RNN uses sequential data and it is a generalization of feed-forward neural networks that has internal memory.
Why do we use LSTM?
Recurrent neural networks RNNs have a long-term dependency issue that LSTM networks were created expressly to address (due to the vanishing gradient problem). LSTMs, in contrast to more conventional feedforward neural networks, feature feedback connections. With this attribute, LSTMs may process whole data sequences, such as time series, without having to treat each data point separately. Instead, they can leverage the information from earlier data points in the sequence to help analyze later data points. Because of this, LSTMs excel at processing data sequences like text, audio, and general time series.
How LSTM Works?
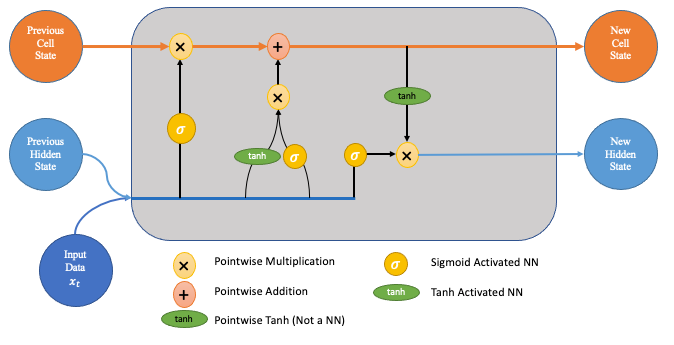
LSTMs utilize several "gates" that regulate how data in a sequence enters, is stored in, and leaves the network. An output gate, an input gate, and a forget gate are the three gates that make up a standard LSTM.
Consider an LSTM cell
as visualized in the following
diagram imagine moving from
left to right.
Forget Gate
The first step is the forget gate. In this step, we will determine which pieces of the cell state—the network's long-term memory—are relevant in light of both the prior hidden state and the fresh incoming data.
Input Gate
The input gate and a new memory network are involved in the following step. This step aims to determine what new information should be added to the network's long-term memory (cell state), given the previous hidden state and new input data.
Note: The input gate and the new memory network are both neural networks in and of themselves, and they both accept identical inputs—the old hidden state and the new input data.
Output gate
The output gate decides the new hidden state. We'll employ three factors—the recently updated cell state, the previous hidden state, and the fresh input data—to make this determination.